二叉树的定义
类型名称:二叉树
数据对象集:一个有穷的结点集合。若不为空,则有根结点和其左、右二叉子树组成。
操作集:BT∈BinTree, Item∈ElementType,重要操作有:
1、Boolean IsEmpty(BinTree BT):判别BT是否为空
2、void Traversal(BinTree BT):遍历,按某顺序访问每个结点
3、BinTree CreateBinTree():创建一个二叉树
常用的遍历方法有:
void PreOrderTraversal(BinTree BT):先序----根、左子树、右子树
void InOrderTraversal(BinTree BT):中序----左子树、根、右子树
void PostOrderTraversal(BinTree BT):后序---左子树、右子树、根
void LevelOrderTraversal(BinTree BT):层次遍历,从上到下、从左到右
二叉树的遍历
(1)先序遍历
遍历过程为:
①访问根结点;
②先序遍历其左子树;
③先序遍历其右子树。
void PreOrderTraversal(BinTree BT){ if(BT) { printf("%d", BT->Data); PreOrderTraversal(BT->Left); PreOrderTraversal(BT->Right); }} 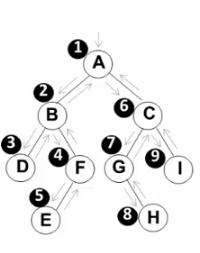
(2)中序遍历
遍历过程为:
①中序遍历其左子树;
②访问根结点;
③中序遍历其右字树。
void InOrderTraversal(BinTree BT){ if(BT) { InOrderTraversal(BT->Left); printf("%d", BT->Data); InOrderTraversal(BT->Right); }} 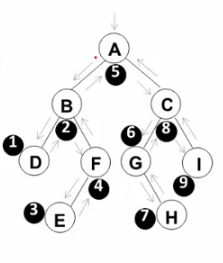
(3)后序遍历
遍历过程为:
①后序遍历其左子树
②后序遍历其右子树
③访问根结点
void PostOrderTraversal(BinTree BT){ if(BT) { PostOrderTraversal(BT->Left); PostOrderTraversal(BT->Right); printf("%d", BT->Data); }} 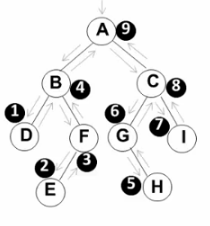
先序、中序、后序遍历过程:遍历过程中经过结点的路线一样,只是各结点的时机不同。
图中在从入口到出口的曲线上用三种符号分别标记了先序、中序和后序访问各结点的时刻。
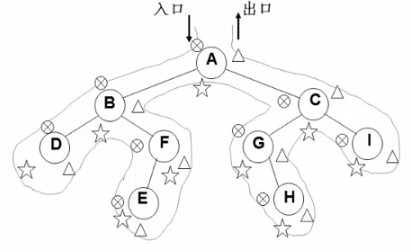
二叉树的非递归遍历
中序遍历非递归遍历算法
非递归算法实现的基本思路:使用堆栈
- 遇到一个结点,就把他压栈,并去遍历它的左子树
- 当左子树遍历结束后,从栈顶弹出这个结点并访问它;
- 然后按其右指针再去中序遍历该结点的右子树。
1 void InOrderTraversal(BinTree BT) 2 { 3 BinTree T = BT; 4 Stack S = CreatStack(MaxSize); /* 创建并初始化堆栈S */ 5 while(T || !IsEmpty(S)) { 6 while(T) { /* 一直向左并将沿途节点压入堆栈 */ 7 Push(S, T); 8 T = T->Left; 9 }10 if(!IsEmpty(S)) {11 T = Pop(S); /* 结点弹出堆栈 */12 printf("%d", T->Data); /* (访问)打印结点 */13 T = T->Right; /* 转向右子树 */14 }15 }16 } 先序遍历:
1 void PreOrderTraversal(BinTree BT) 2 { 3 BinTree T = BT; 4 Stack S = CreatStack(MaxSize); 5 while(T || !IsEmpty(S)) { 6 while(T) { 7 printf("%5d", T->Data); 8 Push(S, T); 9 T = T->Left;10 }11 if(!IsEmpty(S)) {12 T = Pop(S);13 T = T->Right;14 }15 }16 } 后序遍历(暂空):
1 void PostOrderTraversal(BinTree BT) 2 { 3 BinTree T = BT; 4 Stack S1 = CreateStack(MaxSize); 5 Stack S2 = CreateStack(MaxSize); 6 whilie(T||!IsEmpty(S1)) { 7 while(T) { 8 Push(S1, T); 9 Push(S2, T);10 T = T->Right;11 }12 if(!IsEmpty(S1)) {13 T = Pop(S1);14 T = T->Left;15 }16 }17 while(!IsEmpty(S2)) {18 T = Pop(S2);19 printf("%d", T->Data);20 }21 } 思路:对于一个节点而言,要实现访问顺序为左儿子-右儿子-根节点,可以利用后进先出的栈,在节点不为空的前提下,依次将根节点,右儿子,左儿子压栈。
故我们需要按照根节点-右儿子-左儿子的顺序遍历树,而我们已经知道先序遍历的顺序是根节点-左儿子-右儿子,故只需将先序遍历的左右调换并把访问方式打印改为压入另一个栈即可。最后一起打印栈中的元素。
优点是由于利用了先序遍历的思想,代码较简洁,思路较清晰。缺点是需要用一个栈来存储树的所有节点,空间占用较大。
方法二:要访问一个结点的条件上一个访问的结点是右儿子。我们可以增加一个变量Prev来判断当前结点Curr的上一个结点与它的关系来执行相应的操作。
- 若Prev为空(Curr结点是根结点)或者Prev是Curr的父结点,将Curr结点的左孩子和右孩子分别压入栈
- 若Prev是Curr的左儿子,则将Curr右儿子压入栈
- 否则Prev是Curr的右儿子,访问Curr
1 void PostOrderTraversal(BinTree BT) 2 { 3 if(BT == NULL) 4 return ; 5 Stack S = CreatStack(MAX_SIZE); 6 BinTree Prev = NULL , Curr = NULL; //初始化 7 s.push(BT); 8 while(!IsEmpty(S)) 9 {10 Curr = Top(S); //将栈顶元素赋给Curr11 if(Prev == NULL || Prev->Left == Curr || Prev->Right == Curr) //若Prev为NULL或是Curr的父节点12 {13 if(Curr->Left != NULL)14 Push(S, Curr->Left);15 else if(Curr->Right != NULL)16 Push(S, Curr->Right);17 }18 else if(Curr->Left == Prev) //若Prev是Curr的左儿子19 {20 if(Curr->Right != NULL)21 Push(S, Curr->Right);22 }23 else24 {25 printf("%d\n", Curr->Data); //访问当前节点26 Pop(S); //访问后弹出27 }28 Prev = Curr; //处理完当前节点后将Curr节点变为Prev节点29 }30 }
层序遍历:(二叉树遍历的核心问题:二维结构的线性化)
- 从结点访问其左、右儿子结点
- 访问左儿子后,右儿子怎么办?需要存储结构保存暂时不访问的结点。存储结构:堆栈、队列
队列实现:遍历从根结点开始,首先将根结点入队,然后开始执行循环:结点出队、访问该结点、其左右儿子入队,
层序基本过程:先根结点入队,然后:
①从队列中取出一个元素;
②访问该元素所指结点;
③若该元素所指结点的左、右孩子结点非空,则将其左、右孩子的指针顺序入队。
1 void LevelOrderTraversal(BinTree BT) 2 { 3 Queue Q; 4 BinTree T; 5 if(!BT) return; 6 Q = CreatQueue(MaxSize); 7 AddQ(Q, BT); 8 while(!IsEmptyQ(Q)) { 9 T = DeleteQ(Q);10 printf("%d\n", T->Data);11 if(T->Left) AddQ(Q, T->Left);12 if(T->Right) AddQ(Q, T->Right);13 }14 }